Is the math needed by programmers to succeed in AI a surmountable challenge? Many programmers worry that they “can’t do math” and so feel they can’t qualify to work in AI. Often this is a misconception. The analytical skills required to be an efficient programmer are not that far removed from the analytical brain that does well with math.
In this post, we have tried to narrow down the math you will need to the areas of mathematics that would be essential for programmers wanting to work in AI. While the importance of specific mathematical concepts may vary depending on the AI subfield and the specific tasks at hand, the following three areas are generally considered crucial.
- Linear Algebra
- Calculus
- Probability
While proficiency in these areas is necessary, it’s worth noting that specific AI subfields may require additional mathematical knowledge. For example, computer vision may involve knowledge of geometry and image processing, while natural language processing may require some understanding of linguistics and syntax, etc. But we’ll let you cross that bridge when you get there…
Key applications of linear algebra in machine learning
Because linear algebra provides a mathematical framework for understanding and manipulating data, models, and algorithms it plays a fundamental role in machine 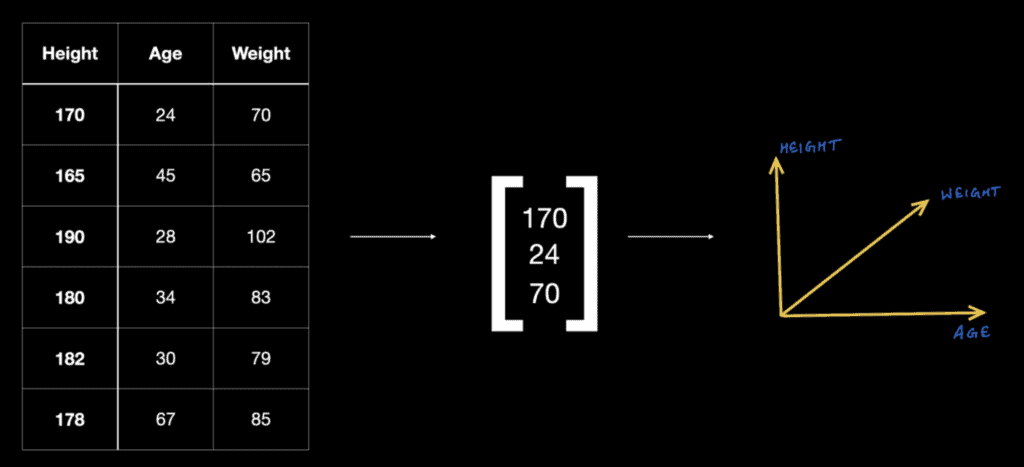
learning. Its principles and operations underpin the core concepts and algorithms used throughout the field, enabling efficient data processing, model development, and optimization.
- Data Representation: Linear algebra allows us to represent and manipulate data efficiently. Data is often represented as matrices or vectors, where each column represents a feature and each row corresponds to an example or observation.
- Matrix Operations: Linear algebra provides various operations that are essential in machine learning, such as matrix multiplication, transpose, inverse, and eigendecomposition. These operations are used in computations involving data transformations, model training, optimization, and dimensionality reduction.
- Linear Models: Many machine learning models, such as linear regression and logistic regression, are based on linear algebra concepts. These models represent relationships between variables using linear equations and utilize matrix operations for estimation and prediction.
- Dimensionality Reduction: Techniques like Principal Component Analysis (PCA) and Singular Value Decomposition (SVD) employ linear algebra to reduce the dimensionality of data while retaining important information. This helps in removing noise, visualizing high-dimensional data, and improving computational efficiency.
- Optimization: Linear algebra is extensively used in optimization algorithms, which are crucial for training machine learning models. Techniques like gradient descent involve computing gradients using linear algebra operations to iteratively update model parameters and minimize the loss function.
- Neural Networks: Deep learning models, specifically neural networks, rely heavily on linear algebra. The computations involved in forward and backward propagation, weight initialization, activation functions, and gradient calculations heavily utilize matrix operations.
- Computer Vision: Linear algebra is used in computer vision tasks, such as image and video processing. Techniques like convolutional neural networks (CNNs) utilize linear algebra operations, such as convolutions and matrix multiplications, to extract features, classify objects, and perform tasks like image recognition and segmentation.
Key applications of calculus in machine learning
Calculus is another essential branch of mathematics that finds wide applications in machine learning. It provides powerful tools for modeling and analyzing the behavior 
of functions and solving optimization problems. Here are some key applications of calculus in machine learning:
- Gradient Descent: Gradient descent is a widely used optimization algorithm in machine learning. It relies on calculus, specifically the concept of gradients, to iteratively update the parameters of a model and minimize a loss function. Calculus enables us to compute derivatives, which indicate the rate of change of a function and helps in finding the direction of steepest descent.
- Backpropagation: Backpropagation is a key algorithm used in training neural networks. It leverages the chain rule from calculus to efficiently compute the gradients of the loss function with respect to the weights and biases in each layer of the network. This enables the adjustment of network parameters during the learning process.
- Cost Function Analysis: Calculus helps in analyzing the behavior of cost functions in machine learning. By finding critical points (where the derivative is zero) and inflection points (where the second derivative changes sign), we can determine the optimal values for model parameters and understand the overall shape of the cost function.
- Optimization and Numerical Methods: Calculus provides various optimization techniques, such as Newton’s and constrained optimization methods, that are used to solve optimization problems in machine learning. These methods involve finding extrema, solving equations, and applying numerical analysis techniques to optimize model performance.
- Integration and Probability: Machine learning often deals with probabilistic models and probability distributions. Calculus, specifically integration, helps in calculating probabilities, evaluating likelihood functions, and performing statistical inference. Techniques like Gaussian integration and Monte Carlo methods rely on calculus for integration and sampling.
- Time Series Analysis: Calculus plays a crucial role in analyzing and modeling time series data. Techniques like differencing, integration, and autoregressive models rely on calculus concepts to understand the trends, seasonality, and dynamics of time-dependent data.
- Reinforcement Learning: Calculus is used in reinforcement learning algorithms, which involve optimizing policies to maximize expected rewards. Techniques like the Bellman equation and value iteration use calculus principles to calculate value functions and update policies.
Calculus helps in optimizing models, understanding function behavior, estimating probabilities, and analyzing time-dependent and sequential data. As you can see above, the mathematical foundations provided by calculus are essential for many core aspects of machine learning research and application.
Key applications of probability in machine learning
Because probability theory is a tool for modeling uncertainty, making predictions, estimating parameters, and reasoning about data it is exceptionally well suited for 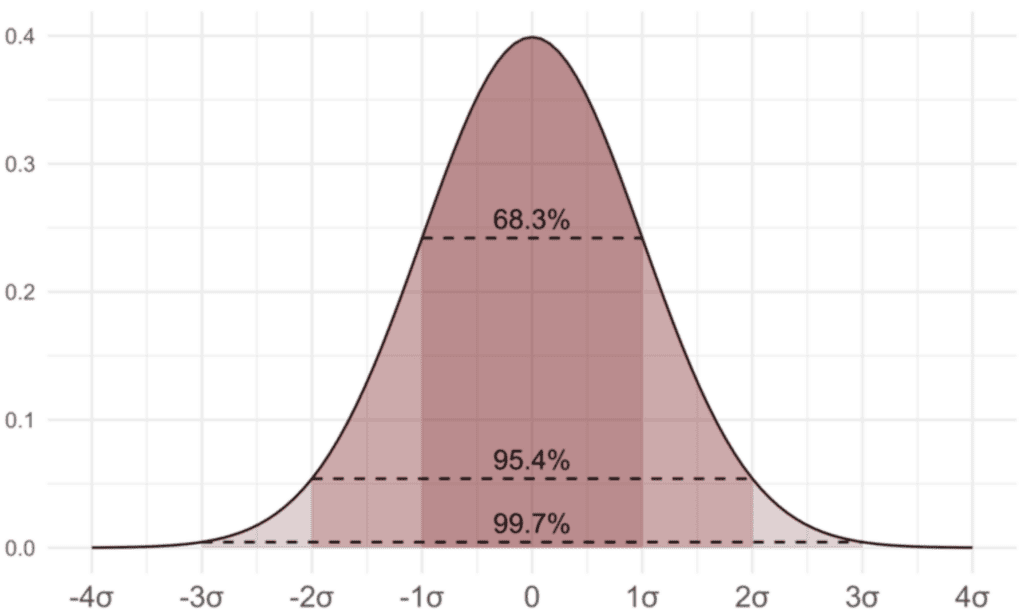
applications in machine learning. Below are some key ways probability can support machine learning projects.
- Statistical Inference: Probability theory forms the basis of statistical inference, which involves making inferences about populations based on sample data. Machine learning algorithms often use statistical inference techniques to estimate parameters, test hypotheses, and quantify uncertainty.
- Probabilistic Modeling: Probabilistic models explicitly represent uncertainty and provide a probabilistic framework for reasoning about data. These models can capture complex relationships and dependencies between variables, allowing for more robust and flexible learning. Examples include Bayesian networks, Markov random fields, and hidden Markov models.
- Bayesian Inference: Bayesian inference is a robust framework for updating beliefs based on observed evidence. It allows for the incorporation of prior knowledge and iterative updating of probabilities as new data is observed. Bayesian methods are used in machine learning for parameter estimation, model selection, and decision-making.
- Probabilistic Graphical Models: Probabilistic graphical models, such as Bayesian networks and Markov random fields, combine probability theory and graph theory to represent complex probabilistic relationships. These models are used for tasks like probabilistic reasoning, uncertainty propagation, and joint probability estimation.
- Uncertainty Estimation: Probability theory provides a natural way to quantify uncertainty in machine learning predictions. By assigning probabilities to different outcomes, models can express confidence levels and provide uncertainty estimates, which is useful for decision-making, risk analysis, and anomaly detection.
- Generative Modeling: Probabilistic models can be used to generate new samples from a learned distribution. This is particularly useful in tasks such as data synthesis, data augmentation, and generative adversarial networks (GANs), where the goal is to generate new data that resembles the training data distribution.
- Reinforcement Learning: Probability theory is utilized in reinforcement learning to model the uncertainty associated with rewards and state transitions. Techniques like Markov decision processes (MDPs) and partially observable Markov decision processes (POMDPs) employ probabilistic models to make sequential decisions and learn optimal policies.
- Bayesian Optimization: Bayesian optimization is a technique used to optimize black-box functions that are expensive to evaluate. It employs probabilistic models to model the objective function and uses Bayesian inference to sequentially select the most promising points for evaluation.
Probability theory provides a formal framework for reasoning under uncertainty, modeling dependencies, and making informed decisions based on data. That is why it plays such a crucial role in many aspects of machine learning, from parameter estimation and model selection to uncertainty estimation and decision-making.
Math for Artificial Intelligence – topic by topic
This is meant to be a suggested “course outline” would you decide you needed a list of topics a bit more detailed than we gave you above. For a great example of the whole content available online we like the AI Math Roadmap. If this one is not to your liking, google “math for AI” and you will have a lot to choose from!
Linear Algebra
Vectors
Matrices
Eigenvalues & eigenvectors
Principle component analysis
Singular value decomposition
Calculus
Functions
Scalar derivative
Gradient
Vector and matrix calculus
Gradient algorithms
Probability
Basic rules and axioms
Random variables
Bayes’ Theorem, MAP, MLE
Popular distributions
Conjugate priors
Markov Chain
Entropy, cross-entropy, KL divergence, mutual information (this may be more Information Theory than straight-up probability theory).
That’s it for today’s AI Math for Programmers. We have a couple of posts that touch on salary ranges in IT as well as the best job opportunities. We also have. for you programmers, a post on how to debug using AI.


